Angr Issue: How to Tackle State Explosion with State Merging
0x00 Intro
Using angr for symbolic execution (symbex) to get assignments done caused anger issues for me and some of my fellows. With due respect, the documentation and existing examples in 2025 are insufficient to quickly teach a newcomer how to correctly tackle state explosion when doing symbex with angr. To fill this niche gap, this post will (1) first dissect an simple example to illustrate why the number of states increases (which will lead to state explosion if not controlled), then (2) try to make sense of and conduct state merging, the trick for tackling state explosion, on the simple example and (3) finally put everything together and try it on a real example that could cause state explosion. Note that it is not guaranteed that the use of angr APIs in this post is ideal. This post intends to provide at least a quick first-aid for those who are stuck with their assignments/CTF challenges with a closing deadline.
0x01 Why the number of states increases
The root cause of state explosion is conditional branches that depend on symbolic conditions. More precisely, if it is feasible with the system of constraints to both take the branch or not to take, Angr will split the current state into two states when executing the branch instruction, corresponding to the two possibilities. Otherwise, angr will be smart enough to not split the state if one of the two possibilities is infeasible.
To show this state-splitting process, I made up a very simple CTF target that expects
command line input starting with k.
#include <stdio.h>
int main(int argc, char *argv[]) {
char *message;
if (argv[1][0] == 'k') {
message = "Congrats!\n";
} else {
message = "Try again\n";
}
printf("%s", message);
return 0;
}
For the sake of reproducibility, the compilation command is
gcc -O0 -g -o simple_branch ./simple_branch.c
Looking at the binary with my favorite Binary Ninja, the CFG of main looks like
this (rebased to 0x400000 as angr uses this as the base address):
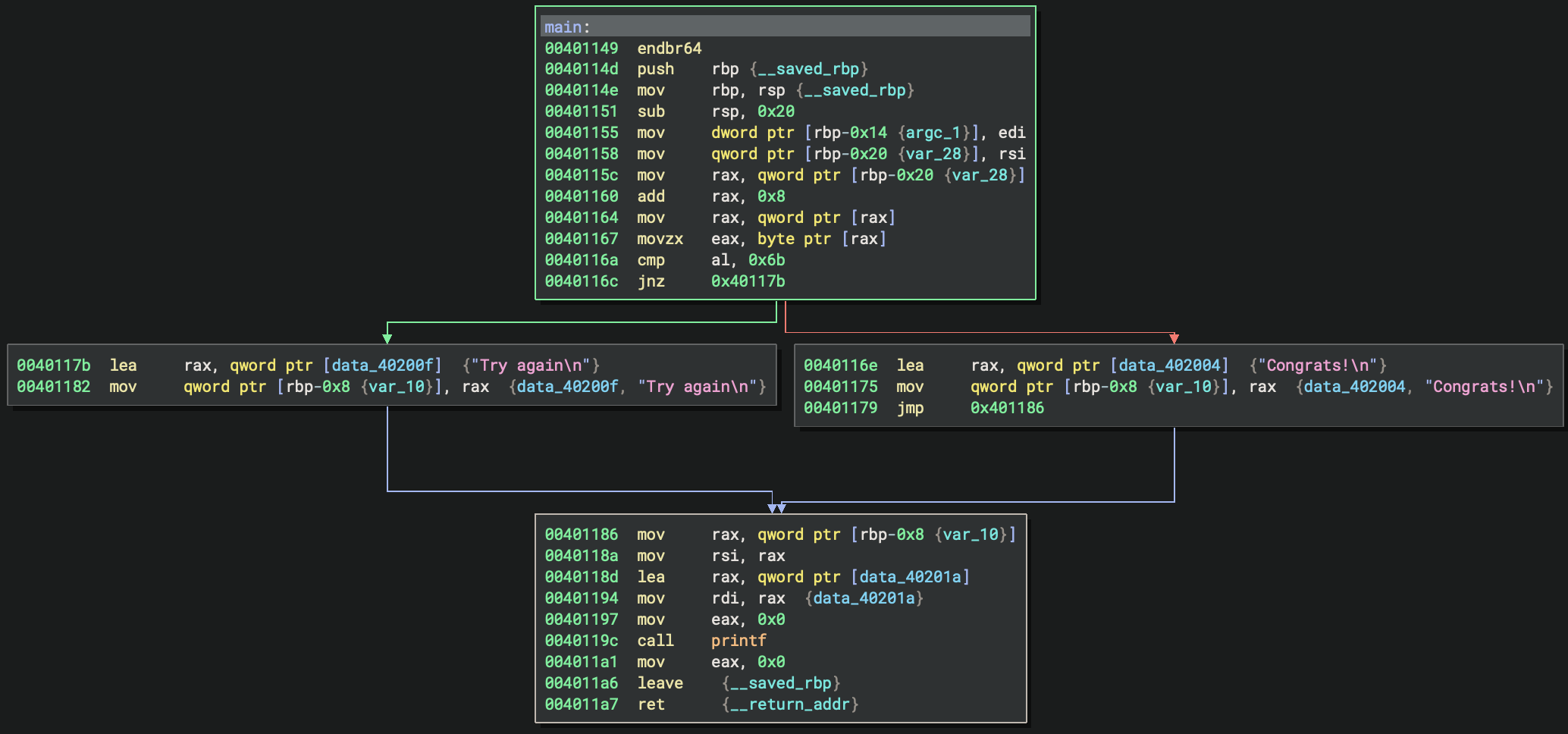
If the state-splitting conjecture is true, then we should see the symbolic execution running with only one state until the end of the basic block at 0x401149 and then splitting into 2 states at 0x40116e and 0x40117b, respectively. The following python script should verify my claim. It is recommended to use Jupyter Notebook to execute the code snippet in cells because I will extend this script later.
# Script 1, Cell 1
import os
import claripy
import angr
# Initialize the symbolic execution
current_dir = os.getcwd()
binary_path = os.path.join(current_dir, "simple_branch")
proj = angr.Project(binary_path, auto_load_libs=False)
sym_var = claripy.BVS("input", 8)
state = proj.factory.entry_state(args=["./simple_branch", sym_var])
simgr = proj.factory.simulation_manager(state)
# Advance till the only state diverges into two
while len(simgr.active) > 0:
simgr.step() # it will execute the whole basic block
print("Number of active states:", len(simgr.active))
for state in simgr.active:
print("\tstate addr", hex(state.addr))
if len(simgr.active) == 2:
break
The output of the script confirms the conjecture.
Number of active states: 1
state addr 0x500000
Number of active states: 1
state addr 0x401149
Number of active states: 2
state addr 0x40116e
state addr 0x40117b
Although in this simple example, the number of states ends up at two and is not exploding at all,
consider an example where there is an if-statement in a loop with 32 iterations. In the first iteration,
it splits into two states, say taken-1 and not-taken-1. Then in the second iteration, taken-1 will split
into two and so does not-taken-1. It is easy to see where this is going to, namely 2^32 states.
0x02 State splitting: A closer examination (contd)
For the sake of completeness, it would be nice to also look at what the constraints look like after the splitting and run the execution all the way till the end.
The script for doing so:
# Script 1, Cell 2
print("\n-- Divergence point reached, checking the constraints --")
# Let's check what the constraints are in the two states
for state in simgr.active:
print("State addr:", hex(state.addr))
print("\tConstraints on sym_var:")
for constraint in state.solver.constraints:
print(f"\t\t{constraint}")
print("\n-- Keep going until the result is printed --")
# 1) One possible way of doing this
# simgr.explore(find=0x4011a1) # states reaching the address will be moved to the 'found' stash
# 2) An alternative way without hardcoding the address:
def until_something_is_printed(sigmr: angr.SimulationManager):
for s in sigmr.active:
if s.posix.dumps(1):
return True
for s in sigmr.deadended:
if s.posix.dumps(1):
return True
return False
# advance states till something is printed in some state(s), then pick them out
# do this until we have no state active
while len(simgr.active) > 0:
simgr.run(stash="active", until=until_something_is_printed)
simgr.move(from_stash="active", to_stash="found", filter_func=lambda s: s.posix.dumps(1))
for state in simgr.found:
print("State advanced to:", hex(state.addr))
print("\tConstraints on sym_var:")
for constraint in state.solver.constraints:
print(f"\t\t{constraint}")
print("\tExpected output:", state.posix.dumps(1).decode('utf-8'))
The output of the cell perfectly aligns with our expectation. If the input is k we enter
the branch that leads to the flag and if not we miss the flag.
-- Divergence point reached, checking the constraints --
State addr: 0x40116e
Constraints on sym_var:
<Bool input_2_8 == 107>
State addr: 0x40117b
Constraints on sym_var:
<Bool input_2_8 != 107>
-- Keep going until the result is printed --
State advanced to: 0x4011a1
Constraints on sym_var:
<Bool input_2_8 != 107>
Expected output: Try again
State advanced to: 0x4011a1
Constraints on sym_var:
<Bool input_2_8 == 107>
Expected output: Congrats!
0x03 Merging the states
If we have too many states, just merge them. What we can do is that after each conditional branch, merging the two states into one so that throughout the execution there will be only one state. But wait a minute, what does it mean by merging the states? An intuitive answer is that a merged state is as if it were the superposition of the two possibilities when going through that conditional branch because the branch depends on some unspecified symbolic values. When it is provided with concrete values or more constraints for those symbolic values, the superposition will suddenly collapse into one, eliminating the other possibility.
If the intuitive answer turns out to be confusing, the following script that observes the constraints after state-merging will hopefully serve as a more explanatory version. The script is still analyzing the simple binary from section 0x01.
# Script 2, cell 1
import os
import claripy
import angr
# Initialize the symbolic execution
current_dir = os.getcwd()
binary_path = os.path.join(current_dir, "simple_branch")
proj = angr.Project(binary_path, auto_load_libs=False)
sym_var = claripy.BVS("input", 8)
state = proj.factory.entry_state(args=["./simple_branch", sym_var],
add_options={angr.options.ZERO_FILL_UNCONSTRAINED_MEMORY,
angr.options.ZERO_FILL_UNCONSTRAINED_REGISTERS})
simgr = proj.factory.simulation_manager(state)
# Advance till the first instruction after the divergence
simgr.explore(find=0x401186)
# Merge the two states
after_merge = simgr.found[0]
for state in simgr.found[1:]:
after_merge,_ ,_ = after_merge.merge(state)
simgr = proj.factory.simulation_manager(after_merge)
assert len(simgr.active) == 1
# print the constraints
for c in simgr.active[0].solver.constraints:
print(c)
The output of the script is below. state_merge_2_8_16 is a new symbolic
variable that describes whether the conditional branch has been taken or not. If
it is taken then the input does not starts with k, otherwise it is a
fall-through and the input starts with k.
<Bool state_merge_2_8_16 == 0x0 || state_merge_2_8_16 == 0x1>
<Bool state_merge_2_8_16 == 0x0 && input_6_8 == 107 || state_merge_2_8_16 == 0x1 && input_6_8 != 107>
To further illustrate what will happen in the end, we run the simulation to the
point right before printf is called. When calling printf("%s",...), RSI
should store the pointer to the message. The idea is to print the possibilities
of the RSI value to confirm that this is indeed the superposition of the two
states (correct input and incorrect input). Finally, a concrete constraint on
the input is supplemented and the superposition is expected to collapse into one.
# Script 2, cell 2
# Stop right before the call to printf
simgr.explore(find=0x40119c)
assert len(simgr.found) == 1
print("Address of current state:", hex(simgr.found[0].addr))
state = simgr.found[0]
rsi_val = state.solver.eval(state.regs.rsi)
print(f"RSI is symbolic: {state.regs.rsi.symbolic}")
# check all possible values of RSI
print(f"\n-- Possible messages to be printed --")
possible_rsi_vals = state.solver.eval_upto(state.regs.rsi, 128)
for val in possible_rsi_vals:
print(f"Possible RSI: {hex(val)}")
message = state.solver.eval(state.memory.load(val, 8), cast_to=bytes)
print(f"Message: {message.decode('utf-8', errors='ignore')}")
print("\n-- Adding constraint on input --")
print(f"RSI is symbolic: {state.regs.rsi.symbolic}")
possible_rsi_vals = state.solver.eval_upto(state.regs.rsi, 128, extra_constraints=[sym_var == b'k'])
for val in possible_rsi_vals:
print(f"Possible RSI: {hex(val)}")
message = state.solver.eval(state.memory.load(val, 8),
cast_to=bytes)
print(f"Message: {message.decode('utf-8', errors='ignore')}")
print("\n-- Running the simulation till the end --")
state.solver.add(sym_var == b'k')
simgr.run(stash='found')
state = simgr.deadended[0]
print(f"Output: {state.posix.dumps(1).decode('utf-8', errors='ignore')}")
The output is self-explanatory. After adding the constraint that input starts
with k, the only possible message to be printed is Congrats, which is the
only satisfiable outcome (state_merge_2_8_16==0x0, branch not taken) after
solving the system of constraints.
Address of current state: 0x40119c
RSI is symbolic: True
-- Possible messages to be printed --
Possible RSI: 0x40200f
Message: Try agai
Possible RSI: 0x402004
Message: Congrats
-- Adding constraint on input --
RSI is symbolic: True
Possible RSI: 0x402004
Message: Congrats
-- Running the simulation till the end --
Output: Congrats!
0x04 Real example that could cause state explosion
The sample iterates the bytes in the command line parameter and determines whether the bytes sum to a magic number. However, there is a twist. To determine the numeric value of each byte, it looks at each bit of the byte and sums the corresponding power of 2 to a partial sum (and later accumulates the partial sum) if the bit at the position is 1. The if-statements in the loop are causing state explosion.
The only thing I want to highlight with this example is that: no matter how the angr API changes in the future, the superposition of a state should always be ready to collapse into any of the possible states in real execution. More specifically, if we examine the partial sum of power-of-2 bits for the byte at the end of each iteration, the partial sum should always evaluate to all values between 0x20 and 0x7E, if we constrain the input to be printable ASCII characters.
// real_example.c
// compile with:
// gcc -O0 -g -o real_example ./real_example.c
#include <stdio.h>
#include <string.h>
int main(int argc, char *argv[]) {
if (argc != 2) {
printf("Usage: %s <input_string>\n", argv[0]);
return 1;
}
char *input = argv[1];
int total_sum = 0;
int str_len = strlen(input);
if (str_len != 32) {
printf("Input string must be exactly 32 characters long.\n");
return 1;
}
for (int i = 0; i < 32; i++) {
unsigned char byte = input[i];
int sum_of_bits = 0;
// Calculate value by summing powers of 2 for each set bit
if (byte & (1 << 0)) sum_of_bits += (1 << 0);
if (byte & (1 << 1)) sum_of_bits += (1 << 1);
if (byte & (1 << 2)) sum_of_bits += (1 << 2);
if (byte & (1 << 3)) sum_of_bits += (1 << 3);
if (byte & (1 << 4)) sum_of_bits += (1 << 4);
if (byte & (1 << 5)) sum_of_bits += (1 << 5);
if (byte & (1 << 6)) sum_of_bits += (1 << 6);
if (byte & (1 << 7)) sum_of_bits += (1 << 7);
total_sum += sum_of_bits;
}
// I'm choosing this because 20040725 is the birthdate of my 推しメン
if (total_sum == 0725 * 04) {
printf("Success: Sum equals %d\n", 0725 * 04);
} else {
printf("Sum is %d, not %d\n", total_sum, 0725 * 04);
}
return 0;
}
The script takes about 2 minutes to run on my laptop, but it should not ended up with state explosion. Some addresses in the binary are hardcoded in the script, check the comments in the script for more details in case it does not run on your machine and fix them accordingly. The indication of success is that, at the end of one iteration, the possible values of the partial sum should be all integers between 0x20 and 0x7E, inclusive.
# Script 3, cell 1
import os
import claripy
import angr
# Initialize the symbolic execution
current_dir = os.getcwd()
binary_path = os.path.join(current_dir, "./real_example")
proj = angr.Project(binary_path, auto_load_libs=False)
sym_var = claripy.BVS("input", 8*33)
state = proj.factory.entry_state(args=["./real_example", sym_var],
add_options={angr.options.ZERO_FILL_UNCONSTRAINED_MEMORY,
angr.options.ZERO_FILL_UNCONSTRAINED_REGISTERS})
# Constraint: the len of the input must be 32 bytes
for idx, char in enumerate(sym_var.chop(8)):
if idx < 32:
state.solver.add(char >= 0x20)
state.solver.add(char <= 0x7e)
else:
state.solver.add(char == 0x00)
simgr = proj.factory.simulation_manager(state)
# the merge points are the first instructions
# where the two divergent paths resulted from a conditional branch meet
# For example, 0x401240 is one such merge point
#
# 00401238 85c0 test eax, eax
# 0040123a 7404 jz 0x401240
# 0040123c 8345f001 add dword ptr [rbp-0x10 {var_18_1}], 0x1
# 00401240 0fb645e7 movzx eax, byte ptr [rbp-0x19 {var_21_1}]
mergepoints = [
0x401240,
0x40124f,
0x40125e,
0x40126d,
0x40127c,
0x40128b,
0x40129a,
0x4012a6,
]
for i in range(32):
for mp in mergepoints:
simgr.explore(find=mp)
for s in simgr.found:
assert s.addr == mp
for s in simgr.active:
assert s.addr == mp
simgr.stash(filter_func=None,
from_stash='found', to_stash='active')
first = simgr.active[0]
the_rest = simgr.active[1:]
for s in the_rest:
first = first.merge(s)[0]
new_simgr = proj.factory.simulation_manager(first)
simgr = new_simgr
state = simgr.active[0]
if i == 0:
rbp = state.regs.rbp
rbp_value = state.solver.eval(rbp)
partial_sum = state.memory.load(rbp_value - 0x10, 4)
possible_values = state.solver.eval_upto(partial_sum, 1024, cast_to=bytes)
# interpret them as integers
possible_values = [int.from_bytes(x, 'little') for x in possible_values]
print(f"Possible values: {sorted(possible_values)}")
print(f'RIP: {hex(state.solver.eval(state.regs.rip))}')
simgr.explore(find=0x4012c3, avoid=0x4012de)
simgr.run(stash='found')
state = simgr.deadended[0]
print(f"Output:{state.posix.dumps(1)}")
possible_inputs = state.solver.eval_upto(sym_var, 4, cast_to=bytes)
for i in possible_inputs:
i = i[:32]
print(f'Possible input: {i.decode("utf-8", errors="ignore")}')
The expected output should is:
Possible values: [0, 1]
RIP: 0x401240
Possible values: [0, 1, 2, 3]
RIP: 0x40124f
Possible values: [0, 1, 2, 3, 4, 5, 6, 7]
RIP: 0x40125e
Possible values: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
RIP: 0x40126d
Possible values: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]
RIP: 0x40127c
Possible values: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]
RIP: 0x40128b
Possible values: [32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126]
RIP: 0x40129a
Possible values: [32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126]
RIP: 0x4012a6
Output:b'Success: Sum equals 1876\n'
Possible input: #+8#~(BA~2*B@_+H(L?@ *%8">,.pP
Possible input: !!` 0AI!'i v&)! =r!`/ o~A}7
Possible input: O*z2_&0"6?"@y> E.0>AD= .0 4v_
Possible input: 1 "! /p ",^A /& HX^of%[Z&SX!`
Trying it out on the binary:
ru1d4@laptop ~/c/b/angr-issue (main) > ./real_example ' #+8#~(BA~2*B@_+H(L?@ *%8">,.pP'
Success: Sum equals 1876